Initialement l’article devait s’intituler: « simulation: une technique scientifique à utiliser avec des pincettes ». Mais il faut reconnaître que le titre actuel est plus accrocheur. Rien de mieux pour aborder un sujet qui me tient à cœur: la simulation informatique… et ses limites.

Rien de plus amusant que de feuilleter des revues de vulgarisation scientifique d’il y a quelques années. On revoit les technologies qui, à l’époque, nous étaient présentées comme révolutionnaires. On y retrouve les certitudes qu’en l’an 2000, tout le monde aura ceci ou cela dans son quotidien. On y glane des photographies avec les supercalculateurs de l’époque dont la puissance équivaut à celle de l’iPad actuel et qui prenaient un volume de trois pièces. On y apprend par exemple qu’en 1993 « France Télécom va investir au Japon pour y développer le Minitel ». En rigolant doucement car en 1994 j’avais ma première adresse mail et utilisait ce qu’à l’époque on appelait un « butineur ». En 1996 Internet avait suffisamment explosé pour que Sciences & Avenir lui consacre un dossier en nous précisant les codes (sic)  à rentrer (en réalité les simples adresses http://…). Pareillement, tous les futurs remplaçant du Concorde qui voleront à mach 2 ou 3 en 2010 nous étaient  présentés… On s’y marre également en revoyant les prévisions et autres simulations  qui sont rarement dans les clous, 20 ans après. De manière générale on s’aperçoit que les prévisions concernant le progrès technique sont toujours trop pessimistes à court terme et trop optimistes à long terme.

Je prendrai pour exemple les années 1990 qui ont été marquées par une prise de conscience environnementale initiée par le problème de la couche d’ozone et l’accident de Tchernobyl. La découverte d’un possible accentuation de l’effet de serre entraînant un réchauffement global du climat a fortement animé le sommet de la Terre à Rio[1]. Admirons les prévisions de l’époque sur le réchauffement du climat qui nous donnaient de très inquiétants +5 à +10 degrés sur l’Europe entre 1990 et 2010-2020. Cela impliquait une certaine augmentation du niveau des mers[2]. Suffisante pour engloutir une grosse partie des Pays-Bas (il suffit d’un mètre pour ce faire).

Ce n’est pas vraiment la sonnette d’alarme qui était tirée, mais plutôt le bourdon de 13 tonnes. Dans cette folie de prédictions désastreuses gravitaient (et gravitent toujours d’ailleurs) d’éminents scientifiques (qui 20 ans avant nous prédisaient un refroidissement généralisé impliquant famines et migration, comme Paul Ehrlich ), et des genres de gourous qui nous ressortent les fameuses théories Gaïa [3]

Vous trouverez d’ailleurs ici une carte interactive permettant de visualiser la perte des territoires suivant la hauteur de la montée des eaux: carte interactive

Rassurons-nous les prévisions de montée des eaux (montée se chiffrant à quelques mm par an depuis le début du XXème siècle et qu’il n’est nullement question ici de contester), s’établissent maintenant à 42 cm pour le 21ème siècle dans le dernier rapport en date (soit déjà la moitié du rapport précédent).

Je ne résiste pas à l’envie de vous donner le lien vers l’archive du JT d’Antenne 2 datant de 1989 qui annonçait que « dans 10 ans des régions entières auront disparues sous les eaux », on pourra y voir toutes les techniques de choc médiatique si aptes à conditionner le téléspectateur et si fausses scientifiquement.

Je ne m’appesantirai pas plus sur cette parenthèse qui n’était là que pour illustrer le propos qui va suivre, d’autres exemples tout aussi marquants auraient pu être pris: nombre de morts prévisionnels du virus du SIDA (notamment en Afrique), ou de la pandémie grippale, population du globe…etc… toutes ces prévisions se sont gourées magistralement à plus ou moins moyen terme.

Comment fonctionne la science prédictive?

Depuis les années 1980 les prédictions sont effectuées (excepté pour Mme Soleil) par simulation de modèle mathématiques via des calculateurs, ou maintenant des ordinateurs. On y gagne beaucoup en rapidité de calcul et en complexité des paramètres à prendre en compte. Ceci dit l’ordinateur est très bête et ne restitue que ce qui a été demandé. C’est aux scientifiques en phase amont d’effectuer un travail préparatoire le plus complet possible pour établir les paramètres pertinents du modèle mathématique. Là réside la première difficulté.

Un exemple simple

Dans le cadre très physique de la simulation d’un champ électrique émis par un doublet élémentaire, on a une relation mathématique simple de type E=Racine(k*P)/D où E est le champ électrique (en V/m), D la distance par rapport à la perpendiculaire du doublet (en m), P la puissance en Watt appliqué au doublet et k=90, un facteur de la relation puissance-champ suivant la géométrie. A partir de ce doublet élémentaire, on peut construire un modèle de base, qui sera dans ce cas appelé antenne isotrope, c’est à dire rayonnant pareillement dans toutes les directions. Ce genre d’antenne n’existe pas, mais permet de servir de modèle de base à partir duquel toutes les autres antennes vont être étudiées. Dans le cadre de cette antenne isotropique, k sera égale à 60 et, si on recherche le champ mesuré, E efficace (c’est à dire dans ce cas Emax divisé par racine de 2) on aura la relation suivante E=racine(30*P)/D.  Aussi pour une puissance de 10W, on aura une mesure de champ de 1,15 V/m à 15 mètres.

caractéristiques du modèle

Sauf que dans la vie, l’électromagnétisme c’est plus compliqué qu’une simple formule.  D’abord parce qu’aucune antenne n’est isotrope (d’une part c’est impossible à construire et d’autre part ça n’a pas grand intérêt), elles ont chacune un modèle de rayonnement qu’on appellera diagramme.  Celui-ci sera donné en fonction du rayonnement isotrope, un peu comme on calcule une variation de prix en fonction d’un indice 100 à une date donnée.  Le diagramme de rayonnement mettra en évidence des directions privilégiées de propagation, des angles d’ouverture…etc… il va donc falloir appliquer un coefficient de correction en fonction du diagramme de rayonnement. Ce sera l’utilité du gain qui servira en quelque sorte de coefficient multiplicateur.

diagramme de rayonnement d’une antenne

Nous avons donc vu la première difficulté qui est de caractériser l’antenne par rapport à un modèle élémentaire existant. Mais il en existe bien d’autres comme nous allons le voir.

Influences pertinentes

En théorie il n’y a pas de différence entre la théorie et la pratique, en pratique, si.

Une fois le modèle plus ou moins caractérisé, il convient de se poser la question des paramètres extérieurs pouvant influencer le résultat. Le scientifique doit déterminer (et justifier) si ces influences peuvent être considérées comme négligeables ou pas. Suivant les situations, seront considérées comme négligeables des contributions inférieures à un dixième, ou un centième, ou encore un millième. C’est le protocole qui décidera.

Pour recenser les influences, on pourra utiliser la méthode d’Ishikawa. Il conviendra de pouvoir quantifier leur importance. Dans le cadre de l’exemple de la propagation du champ électromagnétique, on pourra s’intéresser à différents phénomène physiques connus comme la diffraction, la diffusion, les réflexions multiples et les atténuations qui correspondent au milieu. Sans entrer dans les détails, on se doutera que les bâtiments par exemple, pourraient créer des obstacles atténuant le signal, de même que la pluie ou le brouillard influencent la propagation. Dans le cadre d’une transmission à haute fréquence de courte distance, on pourra supposer que l’activité solaire ou l’état de l’ionosphère n’a que peu d’influence, ce qui ne sera pas le cas par exemple pour les liaisons de plusieurs milliers de kilomètre avec un sous marin en fréquence plus basse.

Notez également que pour quantifier ces phénomènes d’interaction, on fait appel à des modèles théoriques qu’on aura aussi simulé ce qui peut donner un aspect « poupées russes » aux prédictions.

Domaine de validité

Revenons à notre antenne, vous êtes tous prêts maintenant à nous donner le champ électrique  à 25 cm de celle-ci si je vous donne les informations suivantes:

puissance d’entrée 10W

gain (décimal) dans la direction mesurée (en champ): 2,1

influence environnementale de la propagation très faible: 0,99

jetés sur vos calculettes vous me donnez: 144 V/m en me disant que vous avez réussi à prédire le niveau de champ électrique au point donné (sisi je vous entends encore).

Sauf que c’est faux. Votre calcul est sans doute bon, mais le résultat est faux. Tout simplement parce qu’on a oublié un truc essentiel quand on utilise des formules: leur domaine de validité.

Le domaine de validité pour des lignes haute tension n’est pas le même que pour des semi-conducteurs ou des antennes: pourtant il s’agit de champ électromagnétique à chaque fois.

C’est extrêmement important parce que les formules physiques ne se manipulent pas n’importe comment et qu’elles correspondent toujours à des référentiels parfaitement définis. Ainsi, dans le cas qui nous préoccupe, la formule de base n’est valable qu’en zone de champ lointain, c’est à dire à partir d’une certaine  distance de l’émetteur. Distance donnée par des formules impliquant la taille, la géométrie et la fréquence de l’émetteur.  Et c’est la première question qu’on doit se poser quand on se lance dans les calculs: les formules utilisées sont-elles dans leur domaine de validité?

Premier résumé

De notre petit exemple technique on pourra retenir que les études prédictives:

• se fondent sur un modèle élémentaire qui sera caractérisé puis démultiplié ou agrandi (par exemple par la méthode des éléments finis)
• nécessitent de connaître tous les paramètres influents et de pouvoir les quantifier
• nécessitent de vérifier la validité des formules utilisées avec le domaine d’utilisation à chaque étape du processus

On voit déjà poindre les difficultés pour simuler correctement des comportements assez bien définis. Cela ne nous rassure pas concernant des comportements globaux qui ne possèdent pas véritablement de formule magistrale (température moyenne du globe par exemple). Dans certain cas, la formule est crée de toute pièce en utilisant les statistiques ou l’empirisme.

Mais il reste encore de nombreuses choses qui vont influencer  le résultat.

Autres choses à considérer

« Plus que je veux être précis, plus que ça risque d’être faux »

C’est l’adage de toute équipe  planchant sur des simulations. Plus vous cherchez la précision, plus vous avez une chance d’oublier un paramètre influent, plus vous risquez d’avoir la certitude que le résultat est faux. Avec 5 décimales derrière. Mais faux. Il convient toujours de caler son désir de précision avec le besoin réel et les capacités de mesures.  Devant répondre à un gros client institutionnel pour de la simulation, j’ai simplifié au maximum les processus de calcul dans un logiciel développé en partenariat avec le laboratoire de physique d’une grande école. D’autres logiciels existaient, mais coûtaient très chers, nécessitaient 6 mois de formation et surtout nécessitaient d’entrer des données hyper complètes que le client ne maîtrisaient même pas. A part pour faire joli et se la péter, je ne voyais l’intérêt. La plage utile de précision du client étant assez grande, on pouvait simplifier un maximum les hypothèses rendant négligeables de nombreux paramètres sur lesquels nous n’avions aucune information.

En résumé, plus le phénomène est complexe et interdépendant avec d’autres, plus la précision est difficile à obtenir et plus vous risquez de donner des résultats faux.

Et la plage d’incertitude alors?

Ça c’est un truc qui m’énerve au plus au point: on vous donne un résultat ou une valeur mais avec aucune estimation de l’incertitude associée. C’est pourtant essentiel pour comprendre les données!  Les calculs d’incertitude sont très complexes et nécessitent un raisonnement exempt d’erreurs. C’est un peu comme les sondages: on ne vous donne pas les variations possibles en omettant sciemment de préciser que le 24% c’est à plus ou moins 2%…

Normalement tout résultat issu de travaux scientifique est toujours donné avec l‘incertitude liée à son intervalle de confiance. Ce sont les media, les chargés de com’ politique et les charlatans qui omettent systématiquement ces données. Il est vrai que la présentation alourdit la communication, complexifie les chiffres et du coup, entrave la bonne réception du citoyen qui a le QI proche de l’huître (on a des exemples qui sans cesse viennent sonner à la porte de Disons): ainsi une incertitude pourra être donnée en % dans un intervalle de confiance de 95% (c’est généralement la norme). C’est à dire qu’on a 95% de chance que le résultat final soit compris dans l’intervalle donné (24 plus ou moins 2% par exemple) [4].  Bon, avez-vous seulement souvenir d’avoir vu, dans ces publications qui égaient leurs articles d’estimations ou de simulations, une seule donnée concernant l’incertitude des résultats fournis?

L’incertitude en terme de com’ ce n’est pas sexy. Ça laisserait croire qu’on pourrait se tromper, ça insinue le doute alors que la communication doit être efficace et apporter l’adhésion. En terme de com’ ça permet également de ne fournir que le donnée la plus pessimiste (par exemple le niveau des mers montera entre 0,55m et 2m75 en 100 ans, les communicants ont tout intérêt à ne donner que le chiffre le plus élevé); ou le plus optimiste (les prix ne devraient augmenter que de 2,3% cette année…). De même l’incertitude donnée est un excellent moyen pour les scientifiques de critiquer éventuellement le résultat ou la méthode, et exige des justifications que certaines équipes ne sont pas forcément prêtes à donner. Évidemment, plus il y a de paramètres entrant en compte dans le résultat, plus l’incertitude sera complexe à déterminer [5]. Il m’est arrivé d’avoir des simulations avec des incertitudes proches de 100%, ce qui peut paraître insensé dans certains domaines, mais parfaitement viable dans d’autres.

Le biais idéologique

C’est un sujet tabou dans le domaine de la science mais il existe. Vous serez amenés à favoriser les résultats qui vont dans le sens de votre opinion. Il existe évidemment différents degrés, conscients ou non. Par exemple vous pourrez, à travers des milliers de valeurs brutes obtenues, mettre en place une représentation favorisant les valeurs que vous estimez remarquables.  Dans les cas extrêmes, vous pouvez même agir sur les algorithmes pour qu’ils fournissent ce que vous désirez. La pratique est très difficile à évaluer et je ne voudrais pas vous faire croire qu’elle est généralisée, mais juste qu’il est difficile d’effectuer ce genre de travail sans avoir une idée sur le résultat final. Cette envie du résultat peut d’ailleurs être bénéfique. Devant effectuer une simulation, j’obtins des résultats qui ne correspondaient pas vraiment à ce à quoi je m’attendais. Bref la simulation contredisait mon sentiment initial. En reprenant les algorithme, je me suis rendu compte de l’erreur d’inversion de phase sur un paramètre. En rectifiant ceci, j’obtins le résultat  final réaliste (et conforme à mes sentiments), qu’on a pu valider sur le terrain par la suite. Que serait-il passé si je n’avais pas eu d’idée préconçue au départ? Aucune remise en question du résultat certainement.

Un exemple de biais idéologique post-traitement sur la présentation des résultats (donc réalisable par les communiquant et les relais médiatiques).  Il concerne la température du globe, suivant  l’année de référence, il est aisé de déclarer que:

• La température baisse
• La température stagne
• La température augmente
• La température augmente très vite

Ce sont pourtant les mêmes données, relevées par satellite et tout à fait valables [6]

Le problème de la réaction en chaîne

Une difficulté supplémentaire dans la simulation prédictive concerne les éléments à tiroirs insérés dans les boucles de calculs. Quand nos résultat à l’itération n dépendent du résultat obtenu à l’itération n-1, lui même dépendant du n-2 …etc… C’est particulièrement vrai quand on recherche une évolution temporelle. Par exemple le nombre de personnes touchées par une pandémie à l’instant t sera fonction du nombre de personnes contagieuses à l’instant t-1 et donc du nombre de personnes touchées par la pandémie…etc… De même que le réchauffement possible des molécules dépend également de leur état n-1 et de leur température précédente pour avoir un gradient acceptable. Pareillement, la simulation de la population à l’année +50 dépend énormément du résultat de la simulation de la population à l’année +25…

Vous comprenez bien que la moindre erreur ou incertitude sur les premiers degrés de l’itération, va, par réaction en chaîne, rendre le résultat final complètement faux et aberrant. Ayez donc à l’esprit ce petit grain de sable dans une huître qui va, a fil des années, se faire enrober de matière pour devenir, bien plus tard, une belle et grosse perle.

En conclusion

Nous avons vu que les simulations procédaient par mis en place d’un modèle élémentaire caractérisé parfaitement que l’on démultipliait tout en maîtrisant les paramètres influents et les domaines de validité des formules. Les limites de la prédiction, outre le fait de ne pas se tromper sur la caractérisation du modèle, concerne différents facteurs, comme la précision inadaptée, l’intervalle de confiance et le biais idéologique. Enfin, dans le cadre de simulation où les modèles sont interdépendant et calculés de manière itérative, toute imprécision initiale se retrouve amplifiée, faussant tout résultat.

Le doute est donc indispensable quand des estimations ou des simulations vous sont présentées. Non pas le doute bête, idéologique et confortant, mais le véritable doute scientifique qui exclut par exemple tout complot pour s’intéresser à la validité , la pertinence des résultats et surtout,  de leur présentation. Si la science a fait d’énorme progrès dans le domaine de la simulation, il n’en reste pas moins que l’homme est faillible, ce que la machine ne sait pas!

————–

[1] Ce qui est amusant c’est qu’à relire la littérature de l’époque, le méthane et le CO2 étaient tous les deux accusés de participer à l’effet de serre. Et le méthane bien plus (4 fois plus problématique). Entre temps, la planète entière se sera focalisée sur le CO2, bizarrement depuis l’invention des bourses et crédits carbone par des spéculateurs très avisés et qualifiés d’écologistes. Le méthane a donc disparu opportunément des principales préoccupations.

[2] La montée du niveau des mers n’est pas due à la fonte de la banquise du Pôle Nord, ni même à la fonte des glaciers terrestres mais principalement due à la dilatation consécutive à la hausse de la température. Aussi le calcul est particulièrement dépendant de la précision du paramètre de la température globale moyenne des eaux du globe.

[3] Qui considère que la Terre est un organisme vivant dont l’Homme serait un virus. Ne rigolez pas cette théorie a de nombreux adeptes et nombreux relais.

[4] A ce propos je me souviens avoir passé des heures à essayer de faire comprendre à un citoyen « à qui on ne la fait pas et qui s’interroge » ce qu’était un intervalle de confiance à 95% car il estimait (et ça l’arrangeait) que c’était l’incertitude qui était de 95%

[5] Pour simplifier l’incertitude peut être vue comme la somme quadratique des incertitudes élémentaires de chaque paramètre combinées avec leur loi de distribution probabiliste et le coefficient de l’intervalle de confiance.

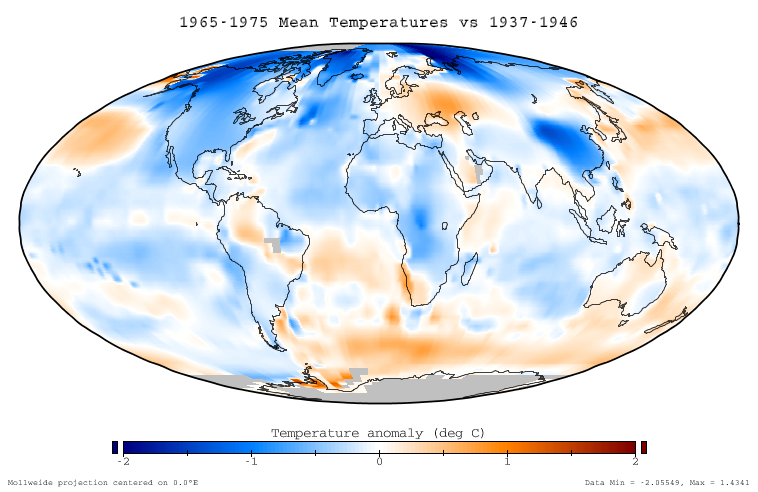
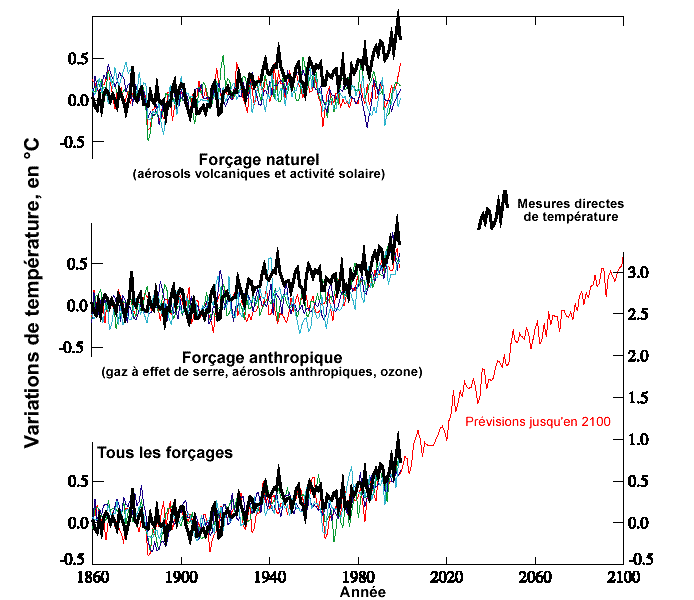
[6] Qu’il est intéressant de comparer avec les simulations effectuées à la fin des années 1990 qui nous sont toujours proposées (on s’aperçoit que la période 2000-2010 est totalement fausse…):

Pour info la variation de température du globe  amenant les scientifiques dans les années 1970 à imaginer une prochaine glaciation: